Painting a Garage

As part of our homework we were given a worksheet to calculate surface area.



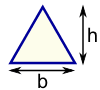
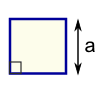
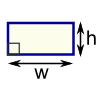
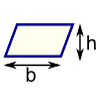
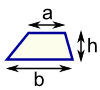
It has a picture of a garage on it, and it says calculate the amount of paint that will be needed to paint it. The walls will be blue and the doors will be white while the windows don't need any paint. To figure this out I first made a copy of the chart they recommended using. However it really only confused me. So I did it the way I found worked best for me. I started with one side and calculated the area of the rectangular wall (and the extra triangle if the wall had one). Then I calculated the area of the doors and windows and subtracted that from the wall calculation. I did that for all of the sides. Then I added up all the blue amounts and squared it and then I did the same for white.

Here is a video that I found helpful when understanding area and surface area.

Formulas for area

What is area?
Area is the size of a particular surface. And each shape has a special formula to calculate it's own area. I know a lot of people struggle with formulas and trying to remember what formula belongs to what shape. So I wanted to make a post that clearly states the name of the simple shape and provides the formula and a visual. I looked on many websites for a picture that would provide all of that information. I found one I really like from mathisfun.com. I originally thought about typing it all out and trying to find a picture to match my examples but this turned out to be much easier and I think a lot clearer. So bellow is the picture I found that clearly states the name of the shape, shows you it, and provides the formula for area.

	Triangle Area = ½ × b × h b = base h = vertical height			Square Area = a2 a = length of side
	Rectangle Area = w × h w = width h = height			Parallelogram Area = b × h b = base h = vertical height
	Trapezoid (US) Trapezium (UK) Area = ½(a+b) × h h = vertical height			Circle Area = π × r2 Circumference = 2 × π × r r = radius
	Ellipse Area = πab			Sector Area = ½ × r2 × θ r = radius θ = angle in radians

I know we have gone over a few in class, but for me (and I hope I am not alone) sometimes when we learn them in class it feels scattered and we hear about them at different times. Which is fine for a lot of people. But I am one of those people that likes to see it all together and visually be able to compare them. It just makes it easier for me to remember them.

Here is a link to the website that provided the photo above.

Right or Not?

In class we did a worksheet to determine if triangles created by sheets of graph paper are acute, right, or obtuse. We lined up three sheets of of different sized graph paper to create a triangle. We then collected data on the numbers of squares or area of a each sheet.



We found the sum of the areas of the two smaller sheets. Then labeled the type of triangle it was. I found that if the sum of the areas of the two smaller sheets is equivalent to the area of the largest sheet then it is a right triangle. If the sum of the two smaller sheets is more than the area of the largest sheet then the triangle is acute. And if the sum of the areas of the two smaller sheets is less than the sum of the area of the largest sheet then the triangle is obtuse. This activity demonstrated the Pythagorean theorem which states that A squared+B squared= C squared.


For more information on the Pythagorean theorem check out this video.