In class we learned about translations, rotations, and reflections. We looked at a website called
brainpop. It was a really cool website however it does cost money which kind of sucks. We saw a cute video of a cartoon boy and a robot that taught us about rotations, translations, and reflections then we took a quiz. We all then got a worksheet where we applied what we had learned.

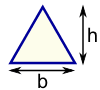
Translation means moving an object or shape to a different location going a certain direction. Reflection means taking and image and flipping it over the mirror line or axis, it is like a mirror image. Rotation means turning an image on a center point a certain direction.